
Back cabin
I’ve read predictions that this winter will be a strong La Niña period, which means that the tropical eastern Pacific Ocean temperature will be colder than normal. The National Weather Service has a lot of information on how this might affect the lower 48 states, but the only thing I’ve heard about how this might affect Fairbanks is that we can expect colder than normal temperatures. The last few years we’ve had below normal snowfall, and I was curious to find out whether La Niña might increase our chances of a normal or above-normal snow year.
Historical data for the ocean temperature anomaly are available from the Climate Prediction Center. That page has a table of “Oceanic Niño Index” (ONI) for 1950 to 2010 organized in three-month averages. El Niño periods (warmer ocean temperatures) correspond to a positive ONI, and La Niña periods are negative. I’ve got historical temperature, precipitation, and snow data for the Fairbanks International Airport over the same period from the “Surface Data, Daily” or SOD database that the National Climate Data Center maintains.
First, I downloaded the ONI index data, and wrote a short Python script that pulls apart the HTML table and dumps it into a SQLite3 database table as:
sqlite> CREATE TABLE nino_index (year integer, month integer, value real);
Next, I aggregated the Fairbanks daily data into the same (year, month) format and stuck the result into the SQLite3 database so I could join the two data sets together. Here’s the SOD query to extract and aggregate the data:
pgsql> SELECT extract(year from obs_dte) AS year, extract(month from obs_dte) AS month,
avg(t_min) AS t_min, avg(t_max) AS t_max, avg((t_min + t_max) / 2.0) AS t_avg,
avg(precip) AS precip, avg(snow) AS snow
FROM sod_obs
WHERE sod_id=’502968-26411’ AND obs_dte >= ’1950-01-01’
GROUP BY year, month
ORDER BY year, month;
Now we fire up R and see what we can find out. Here are the statements used to aggregate October through March data into a “winter year” and load it into an R data frame:
R> library(RSQLite)
R> drv = dbDriver("SQLite")
R> con <- dbConnect(drv, dbname = "nino_nina.sqlite3")
R> result <- dbGetQuery(con,
"SELECT CASE WHEN n.month IN (1, 2, 3) THEN n.year - 1 ELSE n.year END AS winter_year,
avg(n.value) AS nino_index, avg(w.t_min) AS t_min, avg(w.t_max) AS t_max, avg(w.t_avg) AS t_avg,
avg(w.precip) AS precip, avg(w.snow) AS snow
FROM nino_index AS n
INNER JOIN noaa_fairbanks AS w ON n.year = w.year AND n.month = w.month
WHERE n.month IN (10, 11, 12, 1, 2, 3)
GROUP BY CASE WHEN n.month IN (1, 2, 3) THEN n.year - 1 ELSE n.year END
ORDER BY n.year;"
)
What I’m interested in finding out is how much of the variation in winter snowfall can be explained by the variation in Oceanic Niño Index (nino_index in the data frame). Since it seems as though there has been a general trend of decreasing snow over the years, I include winter year in the analysis:
R> model <- lm(snow ~ winter_year + nino_index, data = result)
R> summary(model)
Call:
lm(formula = snow ~ winter_year, data = result)
Residuals:
Min 1Q Median 3Q Max
-0.240438 -0.105927 -0.007713 0.052905 0.473223
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.1000444 2.0863641 1.007 0.318
winter_year -0.0008952 0.0010542 -0.849 0.399
Residual standard error: 0.145 on 59 degrees of freedom
Multiple R-squared: 0.01208, Adjusted R-squared: -0.004669
F-statistic: 0.7211 on 1 and 59 DF, p-value: 0.3992
What does this mean? Well, there’s no statistically significant relationship between year or ONI and the amount of snow that falls over the course of a Fairbanks winter. I ran the same analysis against precipitation data and got the same non-result. This doesn’t necessarily mean there isn’t a relationship, just that my analysis didn’t have the ability to find it. Perhaps aggregating all the data into a six month “winter” was a mistake, or there’s some temporal offset between colder ocean temperatures and increased precipitation in Fairbanks. Or maybe La Niña really doesn’t affect precipitation in Fairbanks like it does in Oregon and Washington.
Bummer. The good news is that the analysis didn’t show La Niña is associated with lower snowfall in Fairbanks, so we can still hope for a high snow year. We just can’t hang those hopes on La Niña, should it come to pass.
Since I’ve already got the data, I wanted to test the hypothesis that a low ONI (a La Niña year) is related to colder winter temperatures in Fairbanks. Here’s that analysis performed against the average minimum temperature in Fairbanks (similar results were found with maximum and average temperature):
R> model <- lm(t_min ~ winter_year + nino_index, data = result)
R> summary(model)
Call:
lm(formula = t_min ~ winter_year + nino_index, data = result)
Residuals:
Min 1Q Median 3Q Max
-10.5987 -3.0283 -0.8838 3.0117 10.9808
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -209.07111 70.19056 -2.979 0.00422 **
winter_year 0.10278 0.03547 2.898 0.00529 **
nino_index 1.71415 0.68388 2.506 0.01502 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.802 on 58 degrees of freedom
Multiple R-squared: 0.2343, Adjusted R-squared: 0.2079
F-statistic: 8.874 on 2 and 58 DF, p-value: 0.0004343
The results of the analysis show a significant relationship between ONI index and the average minimum temperature in Fairbanks. The relationship is positive, which means that when the ONI index is low (La Niña), winter temperatures in Fairbanks will be colder. In addition, there’s a strong (and significant) positive relationship between year and temperature, indicating that winter temperatures in Fairbanks have increased by an average of 0.1 degrees per year over the period between 1950 and 2009. This is a local result and can’t really speak to hypotheses regarding global climate change, but it does support the idea that the effect of global climate change is increasing winter temperatures in our area.
One other note: the model that includes both year and ONI, while significant, explains a little over 20% of the variation in winter temperature. There’s a lot more going on (including simple randomness) in Fairbanks winter temperature than these two variables. Still, it’s a good bet that we’re going to have a cold winter if La Niña materializes.
Thanks to Rich and his blog for provoking an interest in how El Niño/La Niña might affect us in Fairbanks.

Snow on the road
We got 2 inches of snow yesterday (October 26th), so the wait is finally over.
I made the mistake of riding my bicycle to work yesterday, as the snow was falling. It wasn’t too bad on my way in to work, but by the time I left, more than an inch of snow had fallen and the roads hadn’t been plowed. I do have studded, knobby tires on my bicycle, but they’re don’t work very well in situations where the snow is deeper than the tread. I managed to stay upright the whole way home, but it was some white-knuckle, one-wheel drive bicycling.
Note: Yesterday’s first real snowfall was the 8th latest in the 62 year historical record I have access to for the Fairbanks airport station. I'm not sure where the statistics reported in Tuesday’s newspaper came from.
It’s been almost a month since I last discussed the first true snowfall date (when the snow that falls stays on the ground for the entire winter) in Fairbanks, and we’re still without snow on the ground. It hasn’t been that cold yet, but the average temperature is enough below freezing that the local ponds have started freezing. Without snow, there’s a lot of ice skating going on around town. I’m hoping to head out this weekend and do some skating on the pond in the photo above. Still, most folks in Fairbanks are hoping for snow.
Since my last post, I’ve gotten access to data from the National Climate Data Center, and have been working on getting it all processed into a database. I’ve worked out a procedure for processing the daily COOP data, which means I can repeat my earlier snow depth analysis with a longer (and more consistent) data set. The following figure shows the same basic analysis as in my previous post, but now I’ve got data from 1948 to 2008.
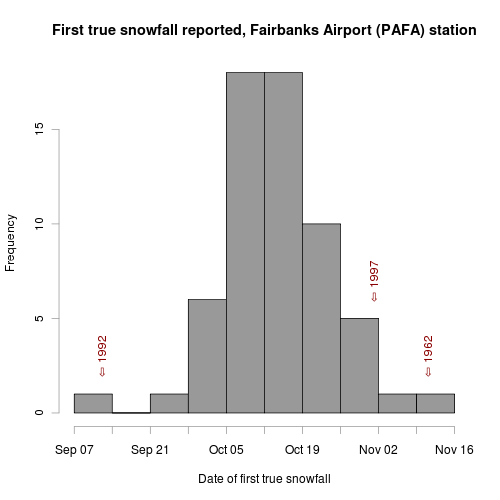
The latest date for the first true snowfall was November 11th, 1962, and we’re almost three weeks away from that date. But we’re also on the right side of the distribution—the mean (and median) date is October 14th, and we’re 9 days past that with no significant snow in the forecast. I’ve also marked the earliest (September 13th, 1992) and latest (November 1st, 1997) first snowfall dates in recent history. 1992 was the year the snow fell while the leaves were still on the trees, causing major power outages and a lot of damage. I think 1997 was the year that we didn’t get much snow at all, which caused a lot of problems for water and septic lines buried in the ground. A deep snowpack provides a good insulating layer that keeps buried water lines from freezing and in 1997 a lot of things froze.
This is also the time of the year when some of the winter birds start making themselves less scarce. We saw our first Pine Grosbeaks of the year, three days later than last year’s first observation, a Northern Goshawk flew over a couple weeks ago, and we got some great views of this Great Horned Owl on Saturday. Andrea took some spectacular photos with her digital camera, and I experimented with my iPhone and the scope we bought in Homer this year. It’s quite a challenge to get the tiny iPhone lens properly oriented with the eyepiece image in the scope, but the photos are pretty impressive when you get it all set up. Even a pretty wimpy camera becomes powerful when looking through a nice scope.
Winter is on it’s way, just a bit late this year. I’ve been taking advantage by riding my bike to work fairly often. Earlier in the week I replaced my normal tires with carbide-studded tires, so I’ll be ready when the ice and snow finally comes.
On Wednesday I reported the results of my analysis examining the average date of first snow recorded at the Fairbanks Airport weather station. It was based on the snow_flag boolean field in the ISD database. In that post I mentioned that examining snow depth data might show the date on which permanent snow (snow that lasts all winter) first falls in Fairbanks. I’m calling this the first “true” snowfall of the season.
For this analysis I looked at the snow depth field in the ISD database for the Fairbanks station. The data was present for the years between 1973 and 1999, but isn’t in the database before that date. I’m not sure why it’s not in there after 1999, but luckily I’ve been collecting and archiving the data in the Fairbanks Daily Climate Summary (which includes a snow depth measurement) since late 2000. Combining those two data sets, I’ve got data for 27 years.
The SQL query I came up with to get the data from the data sets is a good estimate of what we’re interested in, but isn’t perfect because it only finds the date of first snow that lasts at least a week. In a place like Fairbanks where the turn to winter is so rapid and so dependent on the high albedo of snow cover, I think it’s close enough to the truth. Unfortunately, the query is brutally slow because it involves six (!) inner self-joins. The idea is to join the table containing snow depth data against itself, incrementing the date by one day at each join. The result set before the WHERE statement is the data for each date, plus the data for the six days following that date. The WHERE clause requires that snow depth on all those seven dates is above zero. This large query is a subquery of the main query which selects the earliest date found in each year.
There must be a better way to deal with conditions like this where we’re interested in the consecutive nature of the phenomenon, but I couldn’t figure out any other way to handle it in SQL, so here it is:
SELECT year, min(date) FROM
(
SELECT extract(year from a.dt) AS year,
to_char(extract(month from a.dt), '00') ||
'-' ||
ltrim(to_char(extract(day from a.dt), '00')) AS date
FROM isd_daily AS a
INNER JOIN isd_daily AS b
ON a.isd_id=b.isd_id AND
a.dt=b.dt - interval '1 day'
INNER JOIN isd_daily AS c
ON a.isd_id=c.isd_id AND
a.dt=c.dt - interval '2 days'
INNER JOIN isd_daily AS d
ON a.isd_id=d.isd_id AND
a.dt=d.dt - interval '3 day'
INNER JOIN isd_daily AS e
ON a.isd_id=e.isd_id AND
a.dt=e.dt - interval '4 day'
INNER JOIN isd_daily AS f
ON a.isd_id=f.isd_id AND
a.dt=f.dt - interval '5 day'
INNER JOIN isd_daily AS g
ON a.isd_id=g.isd_id AND
a.dt=g.dt - interval '6 day'
WHERE a.isd_id = '702610-26411' AND
a.snow_depth > 0 AND
b.snow_depth > 0 AND
c.snow_depth > 0 AND
d.snow_depth > 0 AND
e.snow_depth > 0 AND
f.snow_depth > 0 AND
g.snow_depth > 0 AND
extract(month from a.dt) > 7
) AS snow_depth_conseq
GROUP BY year
ORDER BY year;
See what I mean? It’s pretty ugly. Running the result through the same R script as in my previous snowfall post yields this plot:
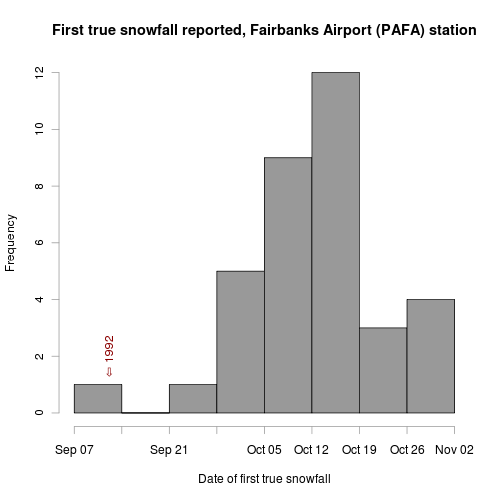
Between 1973 and 2008 we’ve gotten snow lasting the whole winter starting as early as September 12th (that was the infamous 1992), and as late as the first of November (1976). The median date is October 13th, which matches my impression. Now that the leaves have largely fallen off the trees, I’m hoping we get our first true snowfall on the early end of the distribution. We’ve still got a few things to take care of (a couple new dog houses, insulating the repaired septic line, etc.), but once those are done, I’m ready for the Creek to freeze and snow to blanket the trails.
We got our first dusting of snow last night. It stuck around until after noon, allowing me to take the photo on the right when I went for a walk with Nika around the peat bog. You can really tell where the permafrost is by the thick layer of insulating moss that keeps the ground frozen, and is keeping the snow from melting in the photo.
Every year when the first snow falls it seems like it’s earlier than the last, and there’s usually some discussion at the office about how short the summer turned out to be. The early snows of 1992 that knocked out power for days all over town are also normally mentioned. I decided to look and see if I had some data that could place this year’s first snowfall in a historical context.
One of the few free† long-term weather datasets that’s available from the National Climate Data Center is the Integrated Surface Dataset (ISD), which contains daily weather observations for more than 20,000 stations. The Fairbanks Airport station has been in operation for more than 100 years, but it moved in 1946, so I only used data from 1946–2008. In addition to a series of numerical observations (minimum and maximum temperature, pressure, wind speed, etc.), the dataset contains several fields used to indicate whether a particular phenomenon was observed during that day. One of them, snow_flag, is defined as: “True indicates there was a report of snow or ice pellets during the day.”
That’s perfect. Snow depth is another parameter I considered, but this data wasn’t collected until the mid-70s, and it doesn’t really help us answer the question because most of the time the first snowfall of the year doesn’t last long enough to be recorded as snow on the ground.
Here’s the SQL query to find the earliest snowfall date for each year for the Fairbanks Airport station:
SELECT year, min(date) FROM (
SELECT extract(year from dt) AS year,
to_char(extract(month from dt), '00') ||
'-' ||
ltrim(to_char(extract(day from dt), '00')) AS date,
snow_flag
FROM isd_daily
WHERE isd_id = '702610-26411'
AND extract(month from dt) > 7
AND snow_flag = 't'
) AS snow_flag_sub
GROUP BY year
ORDER BY year;
Mix in a little R:
fs <- read.table("first_snow_mm-dd", header=TRUE, row.names=1)
fs$date<-as.Date(fs$date, "%m-%d")
png("first_snow_mm-dd.png", height=500, width=500, units="px", pointsize=12)
hist(fs$date, breaks="weeks", labels=FALSE,
xlab="Date of first snowfall",
main="First snowfall reported, Fairbanks Airport (PAFA) station",
plot=TRUE, freq=TRUE,
ylim=c(0, 20), col="gray60")
text(as.Date("2009-09-23"), 19, "⇦ 2009", srt=90, col="darkred")
dev.off()
And you get this plot:
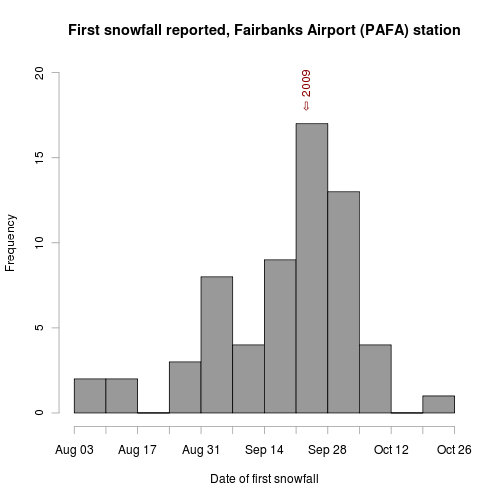
You can see from the plot that the first snowfall comes somewhere between August 3rd and October 26th, with the week of September 21st being the most common. So we’re right on schedule this year.
Another analysis that I’ve been meaning to do is to find the average date when the snow that falls lasts the entire winter. Since I’ve been in Fairbanks, my estimate of this date is the second week of October, but I’ve never actually looked it up to see if that’s true or not. Unfortunately, this requires good snow depth data, and the ISD dataset doesn’t have snow depth for Fairbanks prior to 1975. It’s also a bit more complicated than looking for the earliest snow_flag = 't' because you need to examine future rows to know if the snow depth observation you’re examining lasted more than a few days.
†Why isn’t all the data collected by the Weather Service freely available? Public money was used to collect, analyze, and archive it, so I think it should be made available to the public that paid for it.



