Introduction
This week a class action lawsuit was filed against FitBit, claiming that their heart rate fitness trackers don’t perform as advertised, specifically during exercise. I’ve been wearing a FitBit Charge HR since October, and also wear a Scosche Rhythm+ heart rate monitor whenever I exercise, so I have a lot of data that I can use to assess the legitimacy of the lawsuit. The data and RMarkdown file used to produce this post is available from GitHub.
The Data
Heart rate data from the Rhythm+ is collected by the RunKeeper app on my phone, and after transferring the data to RunKeeper’s website, I can download GPX files containing all the GPS and heart rate data for each exercise. Data from the Charge HR is a little harder to get, but with the proper tools and permission from FitBit, you can get what they call “intraday” data. I use the fitbit Python library and a set of routines I wrote (also available from GitHub) to pull this data.
The data includes 116 activities, mostly from commuting to and from work by bicycle, fat bike, or on skis. The first step in the process is to pair the two data sets, but since the exact moment when each sensor recorded data won’t match, I grouped both sets of data into 15-second intervals, and calculated the mean heart rate for each sensor withing that 15-second window. The result looks like this:
load("matched_hr_data.rdata")
kable(head(matched_hr_data))
| dt_rounded | track_id | type | min_temp | max_temp | rhythm_hr | fitbit_hr |
|---|---|---|---|---|---|---|
| 2015-10-06 06:18:00 | 3399 | Bicycling | 17.8 | 35 | 103.00000 | 100.6 |
| 2015-10-06 06:19:00 | 3399 | Bicycling | 17.8 | 35 | 101.50000 | 94.1 |
| 2015-10-06 06:20:00 | 3399 | Bicycling | 17.8 | 35 | 88.57143 | 97.1 |
| 2015-10-06 06:21:00 | 3399 | Bicycling | 17.8 | 35 | 115.14286 | 104.2 |
| 2015-10-06 06:22:00 | 3399 | Bicycling | 17.8 | 35 | 133.62500 | 107.4 |
| 2015-10-06 06:23:00 | 3399 | Bicycling | 17.8 | 35 | 137.00000 | 113.3 |
| ... | ... | ... | ... | ... | ... | ... |
Let’s take a quick look at a few of these activities. The squiggly lines show the heart rate data from the two sensors, and the horizontal lines show the average heart rate for the activity. In both cases, the FitBit Charge HR is shown in red and the Scosche Rhythm+ is blue.
library(dplyr)
library(tidyr)
library(ggplot2)
library(lubridate)
library(scales)
heart_rate <- matched_hr_data %>%
transmute(dt=dt_rounded, track_id=track_id,
title=paste(strftime(as.Date(dt_rounded,
tz="US/Alaska"), "%b-%d"),
type),
fitbit=fitbit_hr, rhythm=rhythm_hr) %>%
gather(key=sensor, value=hr, fitbit:rhythm) %>%
filter(track_id %in% c(3587, 3459, 3437, 3503))
activity_means <- heart_rate %>%
group_by(track_id, sensor) %>%
summarize(hr=mean(hr))
facet_labels <- heart_rate %>% select(track_id, title) %>% distinct()
hr_labeller <- function(values) {
lapply(values, FUN=function(x) (facet_labels %>% filter(track_id==x))$title)
}
r <- ggplot(data=heart_rate,
aes(x=dt, y=hr, colour=sensor)) +
geom_hline(data=activity_means, aes(yintercept=hr, colour=sensor), alpha=0.5) +
geom_line() +
theme_bw() +
scale_color_brewer(name="Sensor",
breaks=c("fitbit", "rhythm"),
labels=c("FitBit Charge HR", "Scosche Rhythm+"),
palette="Set1") +
scale_x_datetime(name="Time") +
theme(axis.text.x=element_blank(), axis.ticks.x=element_blank()) +
scale_y_continuous(name="Heart rate (bpm)") +
facet_wrap(~track_id, scales="free", labeller=hr_labeller, ncol=1) +
ggtitle("Comparison between heart rate monitors during a single activity")
print(r)
You can see that for each activity type, one of the plots shows data where the two heart rate monitors track well, and one where they don’t. And when they don’t agree the FitBit is wildly inaccurate. When I initially got my FitBit I experimented with different positions on my arm for the device but it didn’t seem to matter, so I settled on the advice from FitBit, which is to place the band slightly higher on the wrist (two to three fingers from the wrist bone) than in normal use.
One other pattern is evident from the two plots where the FitBit does poorly: the heart rate readings are always much lower than reality.
A scatterplot of all the data, plotting the FitBit heart rate against the Rhythm+ shows the overall pattern.
q <- ggplot(data=matched_hr_data,
aes(x=rhythm_hr, y=fitbit_hr, colour=type)) +
geom_abline(intercept=0, slope=1) +
geom_point(alpha=0.25, size=1) +
geom_smooth(method="lm", inherit.aes=FALSE, aes(x=rhythm_hr, y=fitbit_hr)) +
theme_bw() +
scale_x_continuous(name="Scosche Rhythm+ heart rate (bpm)") +
scale_y_continuous(name="FitBit Charge HR heart rate (bpm)") +
scale_colour_brewer(name="Activity type", palette="Set1") +
ggtitle("Comparison between heart rate monitors during exercise")
print(q)
If the FitBit device were always accurate, the points would all be distributed along the 1:1 line, which is the diagonal black line under the point cloud. The blue diagonal line shows the actual linear relationship between the FitBit and Rhythm+ data. What’s curious is that the two lines cross near 100 bpm, which means that the FitBit is underestimating heart rate when my heart is beating fast, but overestimates it when it’s not.
The color of the points indicate the type of activity for each point, and you can see that most of the lower heart rate points (and overestimation by the FitBit) come from hiking activities. Is it the type of activity that triggers over- or underestimation of heart rate from the FitBit, or is is just that all the lower heart rate activities tend to be hiking?
Another way to look at the same data is to calculate the difference between the Rhythm+ and FitBit and plot those anomalies against the actual (Rhythm+) heart rate.
anomaly_by_hr <- matched_hr_data %>%
mutate(anomaly=fitbit_hr-rhythm_hr) %>%
select(rhythm_hr, anomaly, type)
q <- ggplot(data=anomaly_by_hr,
aes(x=rhythm_hr, y=anomaly, colour=type)) +
geom_abline(intercept=0, slope=0, alpha=0.5) +
geom_point(alpha=0.25, size=1) +
theme_bw() +
scale_x_continuous(name="Scosche Rhythm+ heart rate (bpm)",
breaks=pretty_breaks(n=10)) +
scale_y_continuous(name="Difference between FitBit Charge HR and Rhythm+ (bpm)",
breaks=pretty_breaks(n=10)) +
scale_colour_brewer(palette="Set1")
print(q)
In this case, all the points should be distributed along the zero line (no difference between FitBit and Rhythm+). We can see a large bluish (fat biking) cloud around the line between 130 and 165 bpm (indicating good results from the FitBit), but the rest of the points appear to be well distributed along a diagonal line which crosses the zero line around 90 bpm. It’s another way of saying the same thing: at lower heart rates the FitBit tends to overestimate heart rate, and as my heart rate rises above 90 beats per minute, the FitBit underestimates heart rate to a greater and greater extent.
Student’s t-test and results
A Student’s t-test can be used effectively with paired data like this to judge whether the two data sets are statistically different from one another. This routine runs a paired t-test on the data from each activity, testing the null hypothesis that the FitBit heart rate values are the same as the Rhythm+ values. I’m tacking on significance labels typical in analyses like these where one asterisk indicates the results would only happen by chance 5% of the time, two asterisks mean random data would only show this pattern 1% of the time, and three asterisks mean there’s less than a 0.1% chance of this happening by chance.
One note: There are 116 activities, so at the 0.05 significance level, we would expect five or six of them to be different just by chance. That doesn’t mean our overall conclusions are suspect, but you do have to keep the number of tests in mind when looking at the results.
t_tests <- matched_hr_data %>%
group_by(track_id, type, min_temp, max_temp) %>%
summarize_each(funs(p_value=t.test(., rhythm_hr, paired=TRUE)$p.value,
anomaly=t.test(., rhythm_hr, paired=TRUE)$estimate[1]),
vars=fitbit_hr) %>%
ungroup() %>%
mutate(sig=ifelse(p_value<0.001, '***',
ifelse(p_value<0.01, '**',
ifelse(p_value<0.05, '*', '')))) %>%
select(track_id, type, min_temp, max_temp, anomaly, p_value, sig)
kable(head(t_tests))
| track_id | type | min_temp | max_temp | anomaly | p_value | sig |
|---|---|---|---|---|---|---|
| 3399 | Bicycling | 17.8 | 35.0 | -27.766016 | 0.0000000 | *** |
| 3401 | Bicycling | 37.0 | 46.6 | -12.464228 | 0.0010650 | ** |
| 3403 | Bicycling | 15.8 | 38.0 | -4.714672 | 0.0000120 | *** |
| 3405 | Bicycling | 42.4 | 44.3 | -1.652476 | 0.1059867 | |
| 3407 | Bicycling | 23.3 | 40.0 | -7.142151 | 0.0000377 | *** |
| 3409 | Bicycling | 44.6 | 45.5 | -3.441501 | 0.0439596 | * |
| ... | ... | ... | ... | ... | ... | ... |
It’s easier to interpret the results summarized by activity type:
t_test_summary <- t_tests %>%
mutate(different=grepl('\\*', sig)) %>%
select(type, anomaly, different) %>%
group_by(type, different) %>%
summarize(n=n(),
mean_anomaly=mean(anomaly))
kable(t_test_summary)
| type | different | n | mean_anomaly |
|---|---|---|---|
| Bicycling | FALSE | 2 | -1.169444 |
| Bicycling | TRUE | 26 | -20.847136 |
| Fat Biking | FALSE | 15 | -1.128833 |
| Fat Biking | TRUE | 58 | -14.958953 |
| Hiking | FALSE | 2 | -0.691730 |
| Hiking | TRUE | 8 | 10.947165 |
| Skiing | TRUE | 5 | -28.710941 |
What this shows is that the FitBit underestimated heart rate by an average of 21 beats per minute in 26 of 28 (93%) bicycling trips, underestimated heart rate by an average of 15 bpm in 58 of 73 (79%) fat biking trips, overestimate heart rate by an average of 11 bpm in 80% of hiking trips, and always drastically underestimated my heart rate while skiing.
For all the data:
t.test(matched_hr_data$fitbit_hr, matched_hr_data$rhythm_hr, paired=TRUE)
## ## Paired t-test ## ## data: matched_hr_data$fitbit_hr and matched_hr_data$rhythm_hr ## t = -38.6232, df = 4461, p-value < 2.2e-16 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -13.02931 -11.77048 ## sample estimates: ## mean of the differences ## -12.3999
Indeed, in aggregate, the FitBit does a poor job at estimating heart rate during exercise.
Conclusion
Based on my data of more than 100 activities, I’d say the lawsuit has some merit. I only get accurate heart rate readings during exercise from my FitBit Charge HR about 16% of the time, and the error in the heart rate estimates appears to get worse as my actual heart rate increases. The advertising for these devices gives you the impression that they’re designed for high intensity exercise (showing people being very active, running, bicycling, etc.), but their performance during these activities is pretty poor.
All that said, I knew this going in when I bought my FitBit, so I’m not hugely disappointed. There are plenty of other benefits to monitoring the data from these devices (including non-exercise heart rate), and it isn’t a major inconvenience for me to strap on a more accurate heart rate monitor for those times when it actually matters.
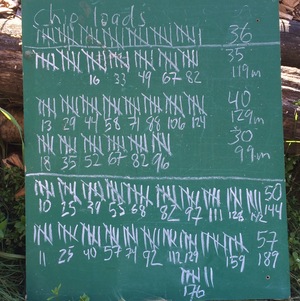
Every couple years we cover our dog yard with a fresh layer of wood chips from the local sawmill, Northland Wood. This year I decided to keep closer track of how much effort it takes to move all 30 yards of wood chips by counting each wheelbarrow load, recording how much time I spent, and by using a heart rate monitor to keep track of effort.
The image below show the tally board. Tick marks indicate wheelbarrow-loads, the numbers under each set of five were the number of minutes since the start of each bout of work, and the numbers on the right are total loads and total minutes. I didn’t keep track of time, or heart rate, for the first set of 36 loads.
It’s not on the chalkboard, but my heart rate averaged 96 beats per minute for the first effort on Saturday morning, and 104, 96, 103, and 103 bpm for the rest. That averages out to 100.9 beats per minute.
For the loads where I was keeping track of time, I averaged 3 minutes and 12 seconds per load. Using that average for the 36 loads on Friday afternoon, that means I spent around 795 minutes, or 13 hours and 15 minutes moving and spreading 248 wheelbarrow-loads of chips.
Using a formula found in [Keytel LR, et al. 2005. Prediction of energy expenditure from heart rate monitoring during submaximal exercise. J Sports Sci. 23(3):289-97], I calculate that I burned 4,903 calories above the amount I would have if I’d been sitting around all weekend. To put that in perspective, I burned 3,935 calories running the Equinox Marathon in September, 2013.
As I was loading the wheelbarrow, I was mentally keeping track of how many pitchfork-loads it took to fill the wheelbarrow, and the number hovered right around 17. That means there are about 4,216 pitchfork loads in 30 yards of wood chips.
To summarize: 30 yards of wood chips is equivalent to 248 wheelbarrow loads. Each wheelbarrow-load is 0.1209 yards, or 3.26 cubic feet. Thirty yards of wood chips is also equivalent to 4,216 pitchfork loads, each of which is 0.19 cubic feet. It took me 13.25 hours to move and spread it all, or 3.2 minutes per wheelbarrow-load, or 11 seconds per pitchfork-load.
One final note: this amount completely covered all but a few square feet of the dog yard. In some places the chips were at least six inches deep, and in others there’s just a light covering of new over old. I don’t have a good measure of the yard, but if I did, I’d be able to calculate the average depth of the chips. My guess is that it is around 2,500 square feet, which is what 30 yards would cover to an average depth of 4 inches.