It’s the beginning of a new year and time for me to look back at what I learned last year. Rather than a long narrative, let’s focus on the data. The local newspaper did a “community profile” of me this year and it was focused on my curiosity about the world around us and how we can measure and analyze it to better understand our lives. This post is a brief summary of that sort of analysis for my small corner of the world in the year that was 2013.
Exercise
2013 was the year I decided to, and did, run the Equinox Marathon, so I spent a lot of time running this year and a lot less time bicycling. Since the race, I’ve been having hip problems that have kept me from skiing or running much at all. The roads aren’t cleared well enough to bicycle on them in the winter so I got a fat bike to commute on the trails I’d normally ski.
Here are my totals in tabular form:
| type | miles | hours | calories |
|---|---|---|---|
| Running | 529 | 89 | 61,831 |
| Bicycling | 1,018 | 82 | 54,677 |
| Skiing | 475 | 81 | 49,815 |
| Hiking | 90 | 43 | 18,208 |
| TOTAL | 2,113 | 296 | 184,531 |
I spent just about the same amount of time running, bicycling and skiing this year, and much less time hiking around on the trails than in the past. Because of all the running, and my hip injury, I didn’t manage to commute to work with non-motorized transport quite as much this year (55% of work days instead of 63% in 2012), but the exercise totals are all higher.
One new addition this year is a heart rate monitor, which allows me to much more accurately estimate energy consumption than formulas based on the type of activity, speed, and time. Riding my fat bike, it’s pretty clear that this form of travel is so much less efficient than a road bike with smooth tires that it can barely be called “bicycling,” at least in terms of how much energy it takes to travel over a certain distance.
Here’s the equations from Keytel LR, Goedecke JH, Noakes TD, Hiiloskorpi H, Laukkanen R, van der Merwe L, Lambert EV. 2005. Prediction of energy expenditure from heart rate monitoring during submaximal exercise. J Sports Sci. 23(3):289-97.
where
- hr = Heart rate (in beats/minute)
- w = Weight (in pounds)
- a = Age (in years)
- t = Exercise duration time (in hours)
And a SQL function that implements the version for men (to use it, you’d replace
the nnn and yyyy-mm-dd with the appropriate values for you):
--- Kcalories burned based on average heart rate and number
--- of hours at that rate.
CREATE OR REPLACE FUNCTION kcal_from_hr(hr numeric, hours numeric)
RETURNS numeric
LANGUAGE plpgsql
AS $$
DECLARE
weight_lb numeric := nnn;
resting_hr numeric := nn;
birthday date := 'yyyy-mm-dd';
resting_kcal numeric;
exercise_kcal numeric;
BEGIN
resting_kcal := ((-55.0969+(0.6309*(resting_hr))+
(0.0901*weight_lb)+
(0.2017*(extract(epoch from now()-birthday)/
(365.242*24*60*60))))/4.184)*60*hours;
exercise_kcal := ((-55.0969+(0.6309*(hr))+
(0.0901*weight_lb)+
(0.2017*(extract(epoch from now()-birthday)/
(365.242*24*60*60))))/4.184)*60*hours;
RETURN exercise_kcal - resting_kcal;
END;
$$;
Here’s a graphical comparison of my exercise data over the past four years:
It was a pretty remarkable year, although the drop in exercise this fall is disappointing.
Another way to visualize the 2013 data is in the form of a heatmap, where each block represents a day on the calendar, and the color is how many calories I burned on that day. During the summer you can see my long runs on the weekends showing up in red. Equinox was on September 21st, the last deep red day of the year.
Weather
2013 was quite remarkable for the number of days where the daily temperature was dramatically different from the 30-year average. The heatmap below shows each day in 2013, and the color indicates how many standard deviations that day’s temperature was from the 30-year average. To put the numbers in perspective, approximately 95.5% of all observations will fall within two standard deviations from the mean, and 99.7% will be within three standard deviations. So the very dark red or dark blue squares on the plot below indicate temperature anomalies that happen less than 1% of the time. Of course, in a full year, you’d expect to see a few of these remarkable differences, but 2013 had a lot of remarkable differences.
2013 saw 45 days where the temperature was more than 2 standard deviations from the mean (19 that were colder than normal and 26 that were warmer), something that should only happen 16 days out of a normal year [ 365.25(1 − 0.9545) ]. There were four days ouside of 3 standard deviations from the mean anomaly. Normally there’d only be a single day [ 365.25(1 − 0.9973) ] with such a remarkably cold or warm temperature.
April and most of May were remarkably cold, resulting in many people skiing long past what is normal in Fairbanks. On May first, Fairbanks still had 17 inches of snow on the ground. Late May, almost all of June and the month of October were abnormally warm, including what may be the warmest week on record in Alaska from June 23rd to the 29th. Although it wasn’t exceptional, you can see the brief cold snap preceding and including the Equinox Marathon on September 21st this year. The result was bitter cold temperatures on race day (my hands and feet didn’t get warm until I was climbing Ester Dome Road an hour into the race), as well as an inch or two of snow on most of the trail sections of the course above 1,000 feet.
Most memorable was the ice and wind storm on November 13th and 14th that dumped several inches of snow and instantly freezing rain, followed by record high winds that knocked power out for 14,000 residents of the area, and then a drop in temperatures to colder than ‒20°F. My office didn’t get power restored for four days.
git
I’m moving more and more of my work into git, which is a distributed revision control system (or put another way, it’s a system that stores stuff and keeps track of all the changes). Because it’s distributed, anything I have on my computer at home can be easily replicated to my computer at work or anywhere else, and any changes that I make to these files on any system, are easy to recover anywhere else. And it’s all backed up on the master repository, and all changes are recorded. If I decide I’ve made a mistake, it’s easy to go back to an earlier version.
Using this sort of system for software code is pretty common, but I’m also using
this for normal text files (the docs repository below), and have
starting moving other things into git such as all my eBooks.
The following figure shows the number of file changes made in three of my
repositories over the course of the year. I don’t know why April was such an
active month for Python, but I clearly did a lot of programming that month. The
large number of file changes during the summer in the docs repository is
because I was keeping my running (and physical therapy) logs in that repository.
Dog Barn
The dog barn was the big summer project. It’s a seven by eleven foot building with large dog boxes inside that we keep warm. When the temperatures are too cold for the dogs to stay outside, we put them into their boxes in the dog barn and turn the heat up to 40°F. I have a real-time visualization of the conditions inside and outside the barn, and because the whole thing is run with a small Linux computer and Arduino board, I’m able to collect a lot of data about how the barn is performing.
One such analysis will be to see how much heat the dogs produce when they are in the barn. To estimate that, we need a baseline of how much heat we’re adding at various temperatures in order to keep it at temperature. I haven’t collected enough cold temperature data to really see what the relationship looks like, but here’s the pattern so far.
The graph shows the relationship between the temperature differential between the outside and inside of the barn plotted against the percentage of time the heater is on in order to maintain that differential, for all 12-hour periods where the dogs weren’t in the barn and there’s less than four missing observations. I’ve also run a linear and quadratic regression in order to predict how much heat will be required at various temperature differentials.
The two r2 values shows how much of the variation in heating is explained by the temperature differential for the linear and the quadratic regressions. I know that this isn’t a linear relationship, but that model still fits the data better than the quadratic model does. It may be that it’s some other form of non-linear relationship that’s not well expressed by a second order polynomial.
Once we can predict how much heat it should take to keep the barn warm at a particular temperature differential, we can see how much less heat we’re using when the dogs are in the barn. One complication is that the dogs produce enough moisture when they are in the barn that we need to ventilate it when they are in there. So in addition to the additive heating from the dogs themselves, there will be increased heat losses because we have to keep it better ventilated.
It’ll be an interesting data set.
Power
Power consumption is a concern now that we’ve set up the dog barn and are keeping it heated with an electric heater. It’s an oil-filled radiator-style heater, and uses around 1,100 Watts when it’s on.
This table shows our overall usage by year for the period we have data.
| year | average watts | total KWH |
|---|---|---|
| 2010 | 551 | 4822 |
| 2011 | 493 | 4318 |
| 2012 | 433 | 3792 |
| 2013 | 418 | 3661 |
Our overall energy use continues to go down, which is a little surprising to me, actually, since we eliminated most of the devices known to use a lot electricity (incandescent light bulbs, halogen floodlights) years ago. Despite that, and bringing the dog barn on line in late November, we used less electricity in 2013 than in the prior three years.
Here’s the pattern by month, and year.
The spike in usage in November is a bit concerning, since it’s the highest overall monthly consumption for the past four years. Hopefully this was primarily due to the heavy use of the heater during the final phases of the dog barn construction. December wasn’t a particularly cold month relative to years past, but it’s good to see that our consumption was actually quite low even with the barn heater being on the entire month.
That wraps it up. Have a happy and productive 2014!
| Device | Watts |
| Time capsule | 12 |
| MacBook Pro | 26 |
| Linux server | 20 |
| Refrigerator | 42 |
| 46" LCD TV | 50 |
| Arctic entryway ventilation fan | 50 |
| Circulating pump | 62 |
| Boot driers | 71 |
| Sewage treatment plant | 350 |
| Jeep heaters | 640 |
| Dakota heaters | 650 |
| Water pump | 1,240 |
| Bedroom heater | 1,500 |
A little over a year ago we bought a whole house energy monitor (The Energy Detective (T.E.D)). It’s got a pair of clamping ammeters that measure the current going through the main power leads inside the breaker panel in our house. This information is transmitted to a small console that we’ve got in the living room, as well as a unit that is connected to our wireless router and displays a web page with the data. I wrote a script that reads this data every minute and stores it in a database. It can also send the data to Google Power if you’re not interested in storing the data yourself.
The console that comes with it runs on rechargeable batteries charged by the cradle it sits in. That means that you can take the console with you to see how much electricity various devices in the house consume. You just watch the display, turn on whatever it is you want to measure, and within a second or two, you can see the wattage increase on the display. We’ve measured the power that the major devices around our house consume, shown in the table on the right.
The lights aren’t in the table. Much of the downstairs is lit with R40 bulbs in ceiling cans, in which we’ve placed 23 Watt CFLs. The most common lighting pattern in the winter is to have the four lights in the kitchen and the single can above the couch on, which is just under 100 Watts. We also have six motion sensing lights, four in the dog yard and one on the shed. Four of these are CFL bulbs (around 20 Watts), and two are outdoor floods (70 Watts). When the dogs are outside in the dark, we’re typically using around 180 Watts to light the dog yard, and the motion sensors also consume some energy even when the bulbs aren’t lit.
Of the devices in the table, we’re always running the sewage treatment plant, the time capsule and the Linux server (around 380 Watts). In winter the circulating pump is running all the time keeping the water and septic lines thawed and we use lights and various other heaters quite a bit more.
Here’s a series of boxplots showing the distribution of our power consumption, by month, for the last year:
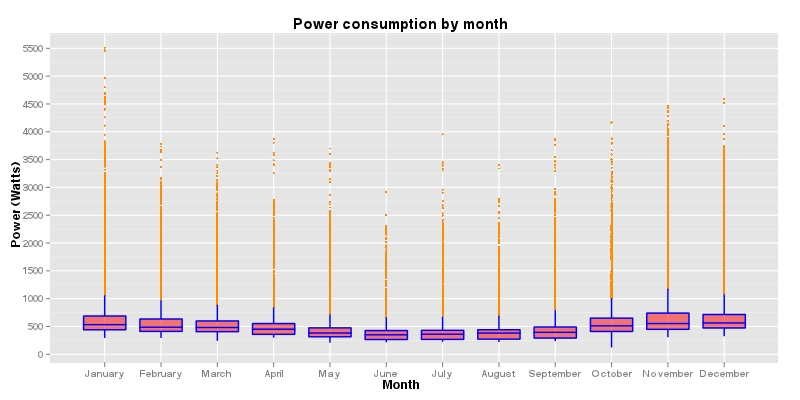
Box and whisker plots show the distribution of a dataset without making any assumptions about the statistical distribution of the data. The box shows the range over which half the points fall (the inter-quartile distance, or IQD), and the horizontal line through the box is the median of the data. For example, in November, over half our power usage falls between about 480 and 750 Watts, with the median consumption just over 500 Watts. If that were the average, we’d use 12 KWHours / day (500 Watts * 24 hours / 1000 Watts/KWatt). The blue vertical lines extending from the boxes (the whiskers) indicate the spread of the majority of the rest of the points. The actual length of these is a somewhat arbitrary 1.5 times the IQD and provides a view of how variable the data is above and below the median. In the case of power consumption, you can tell that the distribution of the points is heavily skewed toward lower consumption values, but that there is a long tail toward higher consumption values. This makes sense when you realize that we’re almost never going to be using less than 380 Watts, but if it’s the dead of winter, our cars are plugged in and the water pump and refrigerator are on, we’ll get a very high spike in our usage. The orange points that extend beyond the whiskers are the actual data values that were outside of the box and whiskers. Again, for this data, we’ve got a lot of these “outliers” because those exceptionally high draw events happen all the time, just not for very long.
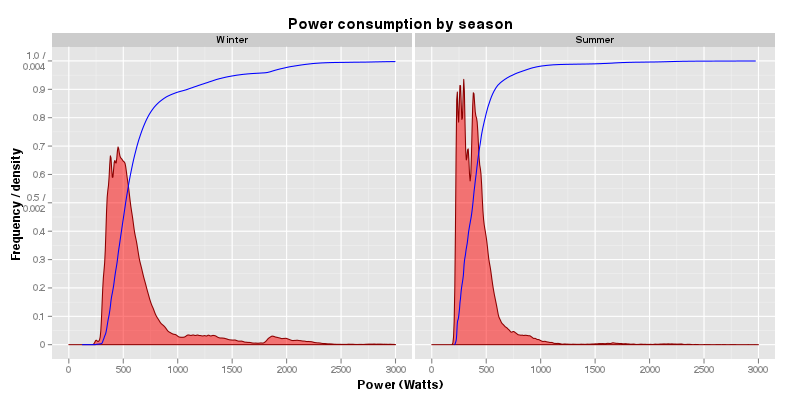
Another way to look at the data is to divide it into summer and winter, and examine the kernel density and cumulative frequency distribution of the data. In this case, the dependent variable (power consumption) is on the x-axis, and we’re looking at how often we’re using that amount of electricity. Looking at the winter density data (the red, solid curve on the left), you can see that there’s a peak just under 500 Watts where most of our usage is, but there’s also smaller peaks around 1,200 Watts and 1,800 Watts. These are probably spikes due to plugging in the vehicle heaters in the morning before we go to work (480 baseline + 640 + 650 = 1,770). The 1,200 Watt peak may be due to just having one vehicle plugged in, or due to the combination of other heaters and the lights being turned on. In summer, there’s a big spike around 350 and a secondary spike around 400. I’m not sure what that cause of that pair of peaks is, but if you look at the monthly density plots, it’s a common pattern for all the summer months. My guess is it’s the baseline sewage treatment plant, plus turning on the lights in the evening. But there aren’t really any other peaks after the distribution drops to close to zero after 1,000 Watts.
The blue line is the cumulative frequency distribution, and it can tell you what percentage of the data points occur on either side of a particular usage value. For example, if you read horizontally across the winter plot from the 0.5 (50%) mark, this intersects the blue line at just over 500 Watts. That means that half of the time, we’re using more than 500 Watts, and half the time we’re using less. The difference between summer and winter is really clear when you look at the cumulative frequency: in summer 95% of our electricity usage is below 750 Watts, but in winter 20% of our usage is above that value.
There’s still a lot more that could be done with all this data. At some point I’d like to relate our usage to other data such as the outside temperature, and I know there are statistical techniques that could help pull apart the total consumption data into it’s individual pieces. For example, as I look at the console right now it’s showing 697 Watts. I know that the sewage treatment plant, stereo, time machine, Linux server, and my laptop are all on. When the ventilation fan goes on, the signal will jump by that amount, and remain at that level until it goes off. Given enough data, these individual, incremental changes in the total consumption should reveal themselves (assuming I actually knew what the technique was, and how to perform the analysis…).
What does all this data really mean? Well, I’m not entirely sure. The idea behind these devices is that they will cause people to use less electricity because they’re getting instant feedback on how what they’re doing affects their usage. The problem is that we’ve already done almost everything what we can do to reduce our usage. Even so, it’s nice to see what’s happening, and a sudden, unexplained spike on the console can let us know when something is on that shouldn’t be.
